22

Have you ever notice the sunset's image in the sea? It's like long light path to the end of the horizon! I've attached a sample of this:

a long light path

How can we explain this? I know that it can happen even in wave less sea or lake! Why is this path so continuous? I expected that sea should act like a mirror!

Chris Mueller
  • 7,033
jack
  • 325
  • 2
    If the waters are realy calm, they are a mirror : https://www.dreamstime.com/stock-image-sunrise-sunset-over-calm-water-image20670601 – anna v Sep 30 '16 at 17:16
  • Yes a mirror would produce a small image of the sun below the horizon, in the water. What's still not at all clear is why that image should spread a lot vertically when the surface ripples, and almost not at all horizontally. – Bob Stein Oct 31 '18 at 14:09
  • Let me spam you with an answer I wrote on the Graphic Design forum. It is a visual explanation. :) https://graphicdesign.stackexchange.com/questions/155722/reflection-of-light-on-water-at-night/155773#155773 – Rafael Feb 28 '23 at 16:42

3 Answers3

12

You'll see an image (or piece of an image) of the Sun anywhere the surface of the water is oriented such that the angle between the Sun and the water and the angle between the water and your eye are equal:

reflection diagram

For water with many ripples, there will be many such locations, but most will be along the line between you and the Sun, or close to it.

In practice, the surface is never perfectly calm, so the effect from ripples always comes into play at least a bit.

I can think of another possible effect that could contribute, even if the water were perfectly calm: on its way in from the Sun, light goes through the atmosphere, which has varying density/temperature, and so also varying refractive index. Now the situation isn't quite so simple as a bunch of parallel rays reflecting off of a mirror. Curved paths through the atmosphere mean that the incident rays are not necessarily parallel, so reflections from different locations (with different incident angles) can meet at a point (the observer). I'd guess that this would be a smaller effect than the ripples, except perhaps for some very contrived weather setups. The effect would still be spreading out mostly along a line between the Sun and observer, since the atmosphere is for the most part varying in the vertical direction (so refraction in a vertical plane).

Kyle Oman
  • 18,441
  • 1
    the waves are quite straight to the observer when they are closer to the beach.but what about the far distances?they don't have a regular direction.so it cant be continuous in the far distances... – jack May 01 '14 at 18:54
  • Well, the wave pattern probably has a preferred orientation no matter where it is. This doesn't need to align in any particular way to get reflection toward the observer in some parts. The wave pattern is quite irregular, so in realistic scenarios there will always be some little piece of water in a reasonably sized region that will reflect toward the observer. – Kyle Oman May 01 '14 at 18:57
  • and I have seen some pictures which there is an quite big angle between the sun and waves direction but the path comes from sun toward the observer again.how do u explain that? – jack May 01 '14 at 19:04
  • 1
    Grab a mirror, hold it horizontally in front of you so that you can see your computer screen (best done by backing up a bit). Now angle the mirror a bit to the side (rotate along an axis oriented along the line between you and the screen). Now your "waves" are not aligned with your "shore". But you can still see the screen (may require a bit of an inclination of the mirror rotating around a horizontal axis perpendicular to the previous one). The waves don't make perfect long lines, so such surface orientations seem reasonable to me. Sadly I don't think I can come up with a clear diagram. – Kyle Oman May 01 '14 at 19:28
7

This is happening because the surface of the sea almost always has a small amount of chop. When the sun is very low on the horizon the amount of angular deflection needed to redirect the light to your eye is very small. All of the tiny little waves caused by wind on the surface of the sea provide a seemingly continuous path to the sun. This is also the reason that the track to the sun is significantly broader than the sun itself.

The effect is more apparent by looking at the sunset over a sea with larger waves such as is shown in the image below. Conversely you can see that the sunset over a body of water with very little chop shows a near mirror like reflection, also illustrated in an image below.

enter image description here

*Image Credit: http://www.billfrymire.com/gallery/sunset-sunrise-ocean-water.jpg.html

enter image description here

*Image Credit: http://footage.shutterstock.com/clip-470437-stock-footage-timelapse-of-golden-sunset-over-lake-muskoka-glassy-surface-on-water-w-clouds-moving-past.html

Chris Mueller
  • 7,033
  • 1
    but why there is just one path?? as u know the waves aren't always toward the beach. we could have another path .why this path is unique ? – jack May 01 '14 at 18:42
  • 1
    @jack That is what I meant by my comment about the path being broader than the sun itself. The deflection from the waves travelling in all directions leads to this broadening of the path. Look at the reflections in my first picture above, and notice that the ones coming from the waves closer to the photographer aren't all in one straight line, they vary a little from right to left. – Chris Mueller May 01 '14 at 18:44
  • I have seen some pictures which there is an angle between the sun and waves direction but the path comes from sun toward the observer again.how do u describe that? – jack May 01 '14 at 18:59
  • 1
    @jack When the sun is very low on the horizon, the large waves don't play a significant role because they deflect the light so much that it doesn't make it to your eye. The amount of deflection needed to get the light to your eye is very small, and this is why many small waves can make a continuous path. This is also why you do not get a significant amount of reflections from the far left or the far right. – Chris Mueller May 01 '14 at 19:04
  • I'm understanding it!the waves act like lots of mirror which has faced to the observer right?the only problem that I should deal with is this :as the waves aren't in a line so there should be a few paths again when there is a angle between sun and waves direction.imagine that there are lined mirrors which have a enough angle to the sun to reflect it's image... – jack May 01 '14 at 19:16
  • thank you for your good answer i'm completely agree with both of u – jack May 01 '14 at 19:32
0

The question is a bit old, but it is fun to answer. Let me make a visual explanation.

  1. Imagine we have a glossy reflective long table with a light at one extreme and the camera on the other side.

enter image description here

  1. Here is a lateral diagram. I drawed a red line conecting the camera and the light. Imagine it is a rope. A "Line of sight rope".

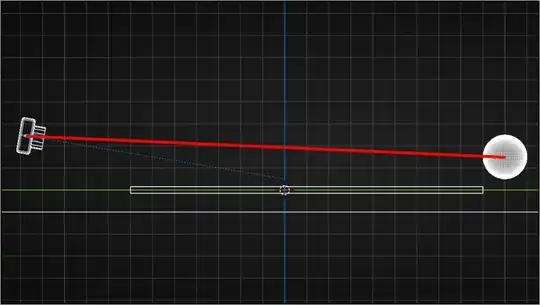
enter image description here

  1. But to really see what is happening let me convert my table into 3 colums of individual square tiles.

enter image description here

  1. We can see that we need to rotate in a very high angle the tiles that are on the sides of the "rope" to see the reflection of the light...

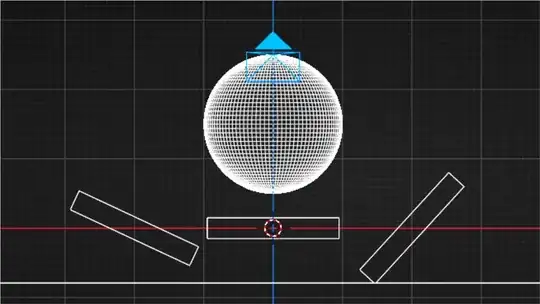
enter image description here

enter image description here

  1. But we can see the reflection on the tiles directly below the rope with very tiny rotations.

enter image description here enter image description here

These angles explain why the "path" of light is formed in the first place.

The question has some parts that are more specific.

I know that it can happen even in wave less sea or lake!... I expected that the sea should act like a mirror!

There is no wave-less sea. It is so big that even tiny waves are always present. So you will not find a mirror-like reflection in the sea.

A lake on the contrary can be waveless if it is isolated enough and there is no wind for some time. You can find some photos of perfect reflections online.

Why is this path so continuous?

How "continuous" is the path depends on several factors.

I will separate this into two characteristics.

A. The longitude.

  • The angle of the Sun with respect to the horizon; The lower on the horizon the longer the path.

  • The camera angle is the same; A drone photo or on the top of a hotel will be shorter.

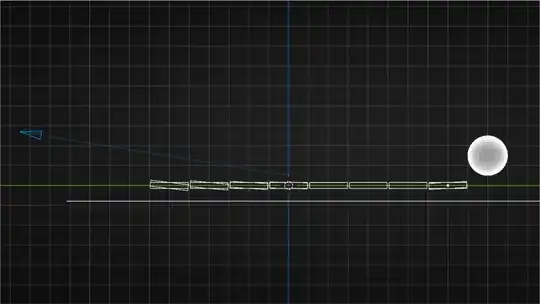
The reason is that with these low angles, close to the reflective surface, the water or the table, the reflection occupies more and more "tiles", because they appear narrower and narrower, and smaller and smaller waves will produce the correct angles necessary to form the reflection.

In this image, I lowered more the camera and the sun, and now, they reflect on all the tiles even without any rotation.

enter image description here

B. The Uniformity.

This depends on the uniformity of the waves. Sometimes we see not a continuous line, but a discontinuous one.

Remember that we can have waves over waves. Tiny ones over bigger ones.

enter image description here

When we think of a calm sea, what we do not have are the big waves, but we do have the tiny ones.

Rafael
  • 171