0

photo

The problem is detailed above. I have worked through problems involving SHM in the horizontal plane, but unsure how to go about it vertically. I know the weight component would need to be incorporated...

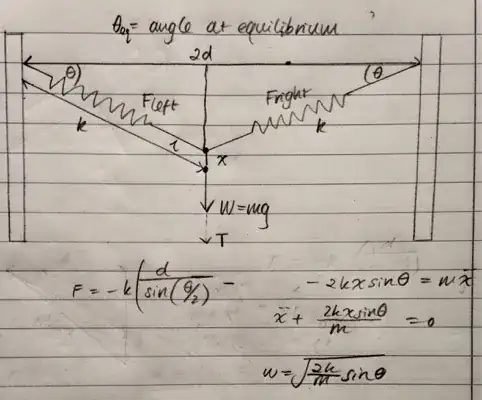
my working Thanks so much for helping!! :)

justbehappy
  • 103
  • 2
    start by drawing the free-body diagram and I'm sure it'll come to you – Phoenix87 Feb 10 '15 at 11:00
  • @Phoenix87 I have tried to work through the problem but it seems the sin(phi) term is inside the sqrt when the answer says its outside...is that right? – justbehappy Feb 10 '15 at 11:36
  • observe that x is not exactly representing the spring elongation – Phoenix87 Feb 10 '15 at 11:56
  • An implicit assumption required to get the same expression is that $d$ is the resting length of the spring, $F_{spring}=k(l-d)$. Otherwise you get a more complicated dependence on $\phi$. – adipy Feb 11 '15 at 15:13

3 Answers3

1

The net force acting on the mass M will be $$F=-2kx\sin\phi$$

Here,x is extension of spring,which can be found out by

$$d=(x+d)\cos\phi$$ $$2d\sin^2\frac{\phi}2=x\cos\phi$$ $$2d\cdot (\frac {\phi}2)^2=x$$...Considering very small oscillations.

Also, $$F=M\frac{d^2((x+d)\sin\phi)}{dt^2}=M\cdot d\cdot\frac{d^2(\tan\phi)}{dt^2}$$

If,we consider the oscillations to be small,then $$\tan \phi \approx \phi,\sin \phi \approx\phi$$

Therefore, $$M\cdot d\cdot\frac{d^2(\phi)}{dt^2}=-2kx\phi$$

But,I am getting

$$\frac{d^2(\phi)}{dt^2}=\frac{-k\phi^3}{M}$$ which is not simple harmonic motion.Also,how can the extremal angle be present in $\omega$ as $\phi$ is changing continuously?

Akshay Bodhare
  • 121
1

Since this is a 1D problem the frequency of small oscillations is simply given by the relation $$\omega^2 = \frac1m U''(x_0),$$ where $U(x)$ is the potential energy of the system and $x_0$ the equilibrium position. This is explicitly given by $$U(x) = mgx + k\left(\sqrt{x^2+d^2}-d\right)^2,$$ and from here one finds $$\omega^2 = \frac{2k}m\left(1-\frac dl + \frac{dx^2}{l^3}\right),$$ where $l^2 = x^2 + d^2$ for convenience. Observe that $d/l = \cos\theta$ and $x/l = \sin\theta$, so that when $x=x_0$, the angle $\theta$ is that of equilibrium, and the above equation is seen to become $$\omega^2 = \frac{2k}m\sin^2\theta.$$

Phoenix87
  • 9,549
0

It does not seem give simple harmonic motion. This can be seen by examining the Lagrangian $$ L = \frac{1}{2} m \dot{x}^2 - 2 \frac{1}{2}k \left(\sqrt{d^2 + x^2} -d \right)^2$$ The factor of two in front of the potential comes from the fact that there are two springs. Now in the limit of $x \ll d$, one has $$ \left(d \sqrt{1+x^2/d^2} -d \right) \approx \frac{1}{2}\left( \frac{x^2}{d}\right)$$ In which case the Lagrangian is $$ L = \frac{1}{2} m \dot{x}^2 - \frac{1}{4}k\left(\frac{x^4}{d^2}\right)$$ Finally, the equation of motion is $$m\ddot{x} = \left(\frac{-k}{d^2}\right)x^3$$ The anharmonicity ultimately comes from the square root dependence of the restoring force on the displacement of the mass $m$.

mwphysics
  • 1