3

Let's say we have a 9 V battery and a wire as shown in the image below:

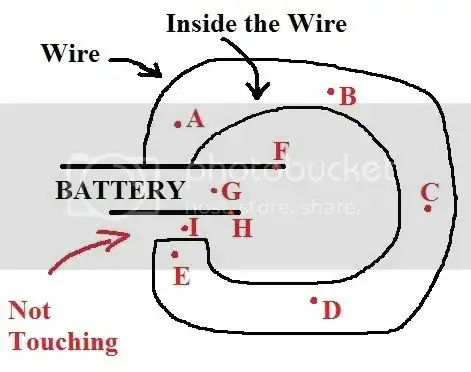
UnconnectedWireQuestion

Let's assume H is the reference for measuring potential. I know the potential in F is 9 V, and I know the electric field in F and H are undefined (this is a controversial thing, I want to avoid that, I don't care for the electric field on F and H). I want to know what is the electric field and electric potential on A, B, C, D, E, G and I, and most importantly, why they assume those values.

I think the electric field is zero on A, B, C, D and E, because otherwise there would be current, which would be odd. I also think the electric potential is constant at those points (consequence of I just said), and equal to the potential in F (which is the battery value, 9 V).

I have no clue for the other points though.

If I'm correct for points A to E, still I have questions regarding them. My thoughts don't really explain why the electric field is zero, it's just that it must be zero, otherwise, something absurd happens. But I can't believe nature "thinks" "oh hey, the field must be zero there, otherwise something absurd will happen". I want an "true" explanation.

I've read this, this and this questions, and learned a lot from them, but in my situation I have an open circuit, and I still can't understand it.

Community
  • 1
Pedro A
  • 529

1 Answers1

3

I think the electric field is zero on A, B, C, D and E, because otherwise there would be current, which would be odd

And you are totally right for an electrostatic system (with no current). Instead of explaining it by, "this would be odd", let's have a look at what happens in the instant you add the wire to the battery pole.:

  1. Before the wire touches the pole, electrons are spread evenly in the wire.
  2. At the instant the wire touches, suddenly the large negative charge at the pole repels the electrons. They move towards the other end. By now there is and electric field $E=\frac{F}{q}$, caused by the battery to move the electrons
  3. After a very short time enough electrons have moved to the other end. Now they repel each other just as much as the repulsion from the pole. In other words, an equal electric field has been set up in the other end cancelling the battery's field. The net field at all points is now zero, and everything is still (electrostatic).

I also think the electric potential is constant at those points

Also true. It's like putting two balls on the same shelf. They will not roll around on this shelv; they would only roll if one shelf was lower than the other. For the charges, there is only an electric potential if they "want to move there".

So with reference to point E or D or C or any other point within the wire, there is no electric potential, since no area has less repulsion than another area. If that would have been the case, it would very quickly be evened out by electrons moving around until that potential has been used up (like the balls rolling until they are as far down as possible, lowering the potential as much as possible.)

I have no clue for the other points though.

If the wire end is very close to an area of lower potential, which seems to be the case, then this acts like a capacitor. The electric field in between the capacitor plates is non-zero. Put a charge there and it will be simultaneously repelled from one side and attracted to the other, and will move. This is the case for point I.

About point G. It is just as for point I, so it depends on the distance between the two plates. But as you say, those plates are in reality a battery and not simply two seperated poles. If point G is inside the battery, then it might experience the so called electromotive force. This is the work done by the battery on the charges at the lower pole to bring them back to the upper pole, ready to move again through the circuit. This is a "potential" in the sense that they are added energy. G must be very specifically located to say anymore though.

and I know the electric field in F and H are undefined (this is a controversial thing, I want to avoid that, I don't care for the electric field on F and H)

Interesting, if you have a link, please provide it :)

Steeven
  • 50,707
  • Awesome answer. You didn't mention point G but I see now that it doesn't matted much, anyway, because it is inside the battery and many things could happen. Thanks again. – Pedro A May 23 '15 at 14:45
  • Regarding the controversial thing: I refer to the often-discussed-topic: "what is the eletric field exactly on the surface of a spherical conductor?". First, please take a look at this other question I asked. This is controversial, in short, because the potential is not differentiable on points at the surface. The points F and H lie, as well, on some sort of "border", so I believe the same problem applies for those points... – Pedro A May 23 '15 at 14:53
  • As I mentioned in a comment in that question, I was able to calculate the electric field on the surface assuming it has a nonzero thickness, and obtained that the electric field increases (approximately) linearly from zero to $\frac{Q}{4\pi\epsilon_0 r^2}$ - which allowed me to understand the question. But if the surface has zero thickness, the problem still stands. Unfortunately, the only link I can provide you is not in English, but in Portuguese (my first language). If you can't read Portuguese, you might at least enjoy the pictures. Thanks! – Pedro A May 23 '15 at 15:02
  • Thanks for the clearification. I see now, undefined on the edge. The Portuguese article is really... Portuguese. I get the point though. – Steeven May 23 '15 at 15:44
  • About point G. It is just as for point I, so it depends the distance between the two plates. But as you say, those plates are in reality a battery and not simply to seperated poles. If point G is inside the battery, then it might experience the so called electromotive force. This is the work done by the battery on the charges at the lower pole to bring them back to the upper pole, ready to move again through the circuit. This is a "potential" in the sense that they are added energy. G must be very specifically located to say anymore though. – Steeven May 23 '15 at 15:47
  • 1
    Yeah. I see, thank you very much. I would upvote more if I could! – Pedro A May 23 '15 at 15:53
  • You are very welcome :) Have a good weekend. – Steeven May 23 '15 at 16:03
  • Matter and Interactions, the book, has a very, very good visual explanation for this. – joshuaronis Aug 14 '18 at 01:52