Why the induced field is ignored in Faraday's law?

Question

Suppose we have a conducting ring in a constant magnetic field $\vec{B}$. Suppose that the ring is being deformed. We know from Faraday's law that such an action will induce a current in the loop. Because of this currect a magnetic field $\vec{B}_{\text{induced}}$ would appear, which will weaken the net magnetic field (Lenz's law). So in total, the magnetic field would change ($\vec{B}+\vec{B}_{\text{induced}}$). However in every texbook there is an assumption that $B$ is always constant, that is: $\mathcal{E}=-\mathrm{d} \Phi/\mathrm{d} t=B(\mathrm{d} A/\mathrm{d} t)$, even though there are induced fields which change the magnetic field. Why do we ignore the induced fields in Faraday's law?

Answer 1

The current generated in the closed wire loop of course induces a magnetic field $B_{induced}$ opposed to $B$ . The magnetic field would be $B-B_{induced}$.

But by what means you keep the constant or anyother initial magnetic field $B$ ???

By an apparatus that, trying to keep the field constant, increases or decreases the strength of its field from $B$ to $B+B_{induced}$ adding or subtracting energy to or from the wire loop depending on its motion and/or deformation. So the field remains constant :$(B+B_{induced})-B_{induced}=B$. That's the Lenz's Law : saves the energy conservation. This is a mechanism of energy exchange.

---

By no way the induced magnetic field $B_{induced}$ could be negleted . By principle, a so called induction motor works because of this :

"ELECTRIC MACHINERY" Fitzgerald-Kingsley-Kusko, 3rd Edition, McGraw-Hill Kogakusha.
4-2 INTRODUCTION TO POLYPHASE INDUCTION MACHINES, pages 187,189

"....the induction motor is one in which alternating current is supplied to the stator directly and to the rotor by induction or transformer action from the stator.(page 187)
.... When used as an induction motor, the rotor terminals are short-circuited......The field produced by the rotor currents therefore revolves at the same speed as the stator field, and a starting torque results, tending to turn the rotor in the direction of rotation of the stator-inducing field. (page 189)

---

Helmholtz Transport Theorem and Faraday's Law

Let $\:\mathbf{F}\left(\mathbf{x},t\right)\:$ be a time-varying vector field defined at points $\:\mathbf{x}=\left( x_{1},x_{2},x_{3}\right)\:$ of a region of $\:\mathbb{R}^{3}\:$ and time $\:t$. If $\:S(t)\:$ is a surface in motion-deformation described by the velocity field $\:\mathbf{w}\left(\mathbf{x},t\right)\:$ of its points, as in Figure, then for the rate of change of the flux of $\:\mathbf{F}\:$ through this surface we have

\begin{equation} \dfrac{\mathrm d}{\mathrm dt}\int\limits_{S(t)}\mathbf{F}\left(\mathbf{x},t\right)\boldsymbol{\cdot} \mathrm d\mathbf{S}=\\ \int\limits_{S(t)} \left[\dfrac{\partial \mathbf{F}}{\partial t} + \left(\nabla \boldsymbol{\cdot} \mathbf{w}\right)\mathbf{F} + \left(\mathbf{w}\boldsymbol{\cdot}\boldsymbol{\nabla}\right)\mathbf{F} - \left(\mathbf{F}\boldsymbol{\cdot} \boldsymbol{\nabla}\right)\mathbf{w}\right] \boldsymbol{\cdot} \mathrm d\mathbf{S} \tag{A-01a} \end{equation}

---

or from this equivalently \begin{equation} \bbox[#E6E6E6,8px]{\dfrac{\mathrm d}{\mathrm dt}\int\limits_{S(t)}\mathbf{F}\left(\mathbf{x},t\right)\boldsymbol{\cdot} \mathrm d\mathbf{S}\:=\:\int\limits_{S(t)} \left[\dfrac{\partial \mathbf{F}}{\partial t} + \left(\nabla \boldsymbol{\cdot} \mathbf{F}\right)\mathbf{w} - \boldsymbol{\nabla} \boldsymbol{\times} \left( \mathbf{w} \boldsymbol{\times} \mathbf{F}\right)\right]\boldsymbol{\cdot} \mathrm d\mathbf{S}} \tag{A-01b} \end{equation} Equation (A-01a) or (A-01b) is known as the Helmholtz transport theorem.
['Generalized Vector and Dyadic Analysis', Chen-To Tai, IEEE PRESS, 2nd Edition 1997 equations (6.11),(6.12) page 119.]

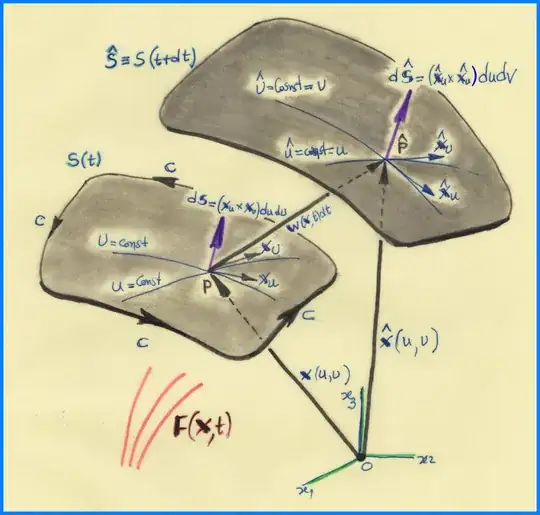
Equation (A-01b) is important for the expression and understanding of Faraday's Law in electromagnetics \begin{equation} \mathrm{emf} \: = \: - \: \dfrac{\mathrm d\Phi}{\mathrm dt} \tag{A-02} \end{equation} that is, the electromotive force $\:(\mathrm{emf})\:$ along a closed path $\:C \:$ equals to the opposite of the time rate of change of the magnetic flux $\:\Phi \:$ passing through any surface $\:S\:$ whose perimeter is the closed path. Note that the surface need not be necessarily stationary but can be in motion and/or under deformation. Now, the magnetic flux $\:\Phi \:$ passing through a surface $\:S\:$ is defined as \begin{equation} \Phi\: \equiv \: \int\limits_{S}\mathbf{B}\left(\mathbf{x},t\right)\boldsymbol{\cdot}\mathrm d\mathbf{S} \tag{A-03} \end{equation} where $\:\mathbf{B}\left(\mathbf{x},t\right)\:$ the magnetic-flux density vector. Replacing $\:\mathbf{F}\:$ by $\:\mathbf{B}\:$ in equation (A-01b) yields \begin{equation} \dfrac{\mathrm d}{\mathrm dt}\int\limits_{S}\mathbf{B}\boldsymbol{\cdot} \mathrm d\mathbf{S}=\int\limits_{S} \left[\dfrac{\partial \mathbf{B}}{\partial t} + \left(\nabla \boldsymbol{\cdot} \mathbf{B}\right)\mathbf{w} - \boldsymbol{\nabla} \boldsymbol{\times} \left( \mathbf{w} \boldsymbol{\times} \mathbf{B}\right)\right] \boldsymbol{\cdot} \mathrm d\mathbf{S} \tag{A-04} \end{equation} and using Maxwell's equations in empty space \begin{align} \boldsymbol{\nabla} \boldsymbol{\times} \mathbf{E} & \:=\:-\:\dfrac{\partial \mathbf{B}}{\partial t} \tag{A-05.1}\\ \nabla \boldsymbol{\cdot}\mathbf{B} & \:=\: 0 \tag{A-05.2} \end{align}
equation (A-04) yields \begin{equation} \int\limits_{S} \boldsymbol{\nabla} \boldsymbol{\times}\left[\mathbf{E} + \left( \mathbf{w} \boldsymbol{\times} \mathbf{B}\right)\right] \boldsymbol{\cdot} \mathrm d\mathbf{S} \:=\:-\:\dfrac{\mathrm d}{\mathrm dt}\int\limits_{S}\mathbf{B}\boldsymbol{\cdot} \mathrm d\mathbf{S}\: = \: - \: \dfrac{\mathrm d\Phi}{\mathrm dt} \tag{A-06} \end{equation}

By Stoke's Theorem \begin{equation} \int\limits_{S} \boldsymbol{\nabla} \boldsymbol{\times}\left[\mathbf{E} + \left( \mathbf{w} \boldsymbol{\times} \mathbf{B}\right)\right] \boldsymbol{\cdot} \mathrm d\mathbf{S} \: = \: \oint\limits_{C} \left[\mathbf{E} + \left( \mathbf{w} \boldsymbol{\times} \mathbf{B}\right)\right]\boldsymbol{\cdot} \mathrm d\mathbf{L} \tag{A-07} \end{equation} so \begin{equation} \oint\limits_{C} \left[\mathbf{E} + \left( \mathbf{w} \boldsymbol{\times} \mathbf{B}\right)\right]\boldsymbol{\cdot} \mathrm d\mathbf{L} = \: - \: \dfrac{\mathrm d\Phi}{\mathrm dt} \tag{A-08} \end{equation}

and the electromotive force $\:(\mathrm{emf})\:$ along a closed path $\:C \:$ is \begin{equation} \bbox[#FFFF88,5px,border:1px solid black]{\mathrm{emf}\;=\: - \: \dfrac{\mathrm d\Phi}{\mathrm dt}=\;\oint\limits_{C} \left[\mathbf{E} + \left( \mathbf{w} \boldsymbol{\times} \mathbf{B}\right)\right] \boldsymbol{\cdot} \mathrm d\mathbf{L}} \tag{A-09} \end{equation}

Note that the expression $\:\left[\mathbf{E} + \left( \mathbf{w} \boldsymbol{\times} \mathbf{B}\right)\right] \:$ is the Lorentz force on a unit electric charge moving with velocity $\:\mathbf{w} \:$.
The electromotive force $\:(\mathrm{emf})\:$ along a closed path $\:\:C\:\:$ defined by (A-09) may be separated into two parts

(1) one part called transformer electromotive force $\:(\mathrm{emf})_{transformer}\:$ \begin{equation} (\mathrm{emf})_{transformer}\;\stackrel{\text{def}}{\equiv}\;\oint\limits_{C} \mathbf{E}\boldsymbol{\cdot} \mathrm d\mathbf{L} =\;-\;\int\limits_{S}\dfrac{\partial \mathbf{B}}{\partial t} \boldsymbol{\cdot} \mathrm d\mathbf{S} \tag{A-10} \end{equation} due to the time rate of change of $\:\mathbf{B}\:$ and

(2) another part called motional electromotive force $\:(\mathrm{emf})_{motional}\:$ \begin{equation} (\mathrm{emf})_{motional}\;\stackrel{\text{def}}{\equiv}\;\oint\limits_{C}\left( \mathbf{w} \boldsymbol{\times} \mathbf{B}\right) \boldsymbol{\cdot} \mathrm d\mathbf{L} = \int\limits_{S} \boldsymbol{\nabla} \boldsymbol{\times} \left( \mathbf{w} \boldsymbol{\times} \mathbf{B}\right) \boldsymbol{\cdot} \mathrm d\mathbf{S} \tag{A-11} \end{equation} due to the motion and/or deformation of the closed path.

This separation of the emf into the two parts, one due to the time rate of change of $\:\mathbf{B}\:$ and the other to the motion of the closed path, is somewhat arbitrary in that it depends on the relative velocity of the observer and the system (and in any case isn't Lorentz invariant).

---

'The Feynman Lectures on Physics' - Mainly Electromagnetics & Matter,Volume 2, New Millennium Edition, Basic Books . Chapter 17 : The Laws of Induction, 17-2 Exceptions to the "flux rule", page 17-2

"We begin by making an important point: The part of the emf that comes from the $\mathbf{E}$-field does not depend on the existence of a physical wire (as does the $\mathbf{w} \boldsymbol{\times} \mathbf{B}$ part). The $\mathbf{E}$-field can exist in free space, and its line integral around any imaginary line fixed in space is the rate of change of the flux of $\mathbf{B}$ through that line. (Note that this is quite unlike the $\mathbf{E}$-field produced by static charges, for in that case the line integral of $\mathbf{E}$ around a closed loop is always zero.)"

Answer 2

To answer the question in your title, it is not ignored. Faraday's law relates the total magnetic induction time derivative at a point to the electric field's curl, or, in the EMF form you've given, the rate of change of total flux through a loop to the EMF around the loop.

It is often assumed, though, that $B_{induced}$ is small compared to the known magnetic field assumed to be giving rise to the EMF. Thus, the assumption holds good for a loop of high resistance: not much current can flow. Often physics problems in electromagnetism want you to assume no current: so you're calculating the "open circuit" EMF.

However, the induced or reaction field is often not negligible. In an inductor, for example, the induced field is responsible for the back EMF that opposes the current and is the origin of the reactance term $i\,\omega\,L$.

Answer 3

Because at the fundamental level, there is no induced field. EMF is electromotive force.

To understand this, simplify the situation down to a single electron. It has an electromagnetic field. If however you were a charged particle with no initial relative motion with respect to the electron, you would experience only linear force towards or away from it, and you might claim that it has an electric field. But if you had some initial relative motion past the electron, you would also experience rotational force, and you might claim the electron has a magnetic field too. But you don't change the electron's field merely by moving past it. Because the Lorentz force is "the combination of electric and magnetic force", and it's "due to electromagnetic fields". Yes, people are forever talking about electric fields and magnetic fields, but see section 11.10 of Jackson's Classical Electrodynamics where he says "one should properly speak of the electromagnetic field F$_{\mu\nu}$ rather than E or B separately". Or see the Wikipedia electromagnetic field article: which says "over time, it was realized that the electric and magnetic fields are better thought of as two parts of a greater whole - the electromagnetic field". As to how it works, see what Minkowski said in Space and Time:

"In the description of the field caused by the electron itself, then it will appear that the division of the field into electric and magnetic forces is a relative one with respect to the time-axis assumed; the two forces considered together can most vividly be described by a certain analogy to the force-screw in mechanics; the analogy is, however, imperfect".

Note how he said the field? It's the electromagnetic field, and electromagnetic field interactions result in linear electric force and rotational magnetic force. It works something like a screw-thread: you push current up a wire and the motor turns, or you turn the dynamo to push current up a wire. Maxwell talked about this too, see On Physical Lines of Force:

"a motion of translation along an axis cannot produce a rotation about that axis unless it meets with some special mechanism, like that of a screw".

It's like a screw because the electron has a spinor nature. Maxwell didn't know about spinors, or frame-dragging, or even electrons. But his was "The Theory of Molecular Vortices applied to Magnetic Phenomena". And as you are doubtless aware, co-rotating vortices repel, whilst counter-rotating vortices attract. And they go round each other too. Check out positronium. Things get more complicated when you have electrons and metal ions in wire, more complicated again for current in two wires, and more complicated again when you wrap one wire into a solenoid and another into a loop. But you can work up to that.