Will Gauss's law still hold in case of deviation from inverse square law?

Question

Assume a spherical metallic shell over which a charge $Q$ is distributed uniformly.

Applying Gauss's law $\displaystyle\oint\textbf{E}\cdot d\textbf{a}=\frac{Q_{\text{enc.}}}{\epsilon_0}$ by considering a gaussian spherical surface concentric with the shell but with smaller radius, one can easily show that the electric field inside the shell is 0 since there is no enclosed charge within the gaussian surface.

What would change in the above analysis and result had the electrostatic interaction been different from the inverse square behavior (i.e., $1/r^{2+\epsilon}$ instead of $1/r^2$)?

Answer 1

You can't combine Gauss's law with different force laws than $|\vec E|\sim Q/r^2$ because $|\vec E|\sim Q/r^2$ actually follows from Gauss's law! It's because of the very equation you wrote down, $$ \epsilon_0\int \vec{dS}\cdot \vec E = Q_{\rm inside} $$ When $\vec E$ is radial and spherically symmetric, the left hand side is equal to $4\pi R^2$ from the area times $|\vec E|$ which implies that $|\vec E|$ goes like $1/r^2$. So the assumptions of your problem can never be realized and your question makes no sense.

In different number of spatial dimensions $D$, $1/r^{2}$ is replaced by $1/r^{d-1}$.

Answer 2

As discussed in another question (and I see that Lubos has touched on this as well), Coulomb's law is considered to be a consequence of Gauss's law in 3D space. If physical conditions were to change such that it and Coulomb's law became inconsistent with each other, Gauss's law would continue to hold, and Coulomb's law is the one that would need to be modified. So any deviation of the exponent in Coulomb's law from $-2$ would probably be taken as an indication of something funky going on with the dimensionality of space, not that Gauss's law is broken.

But for educational purposes, you could calculate what would happen if we throw Gauss's law out the window, and then postulate that, despite being in 3D space, Coulomb's law has an exponent other than $-2$ on the radius for some bizarre reason. Wikipedia has an article on the shell theorem which includes a derivation that applies almost unchanged to this case. (They do it for gravity, so for our purposes, just mentally replace the masses $M,m$ with charges $Q,q$.)

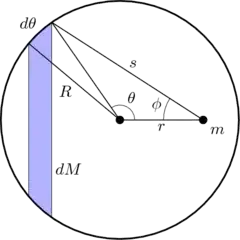
The charge within the shaded band is

$$\mathrm{d}Q = \frac{Q}{4\pi R^2} (2\pi R\sin\theta)(R\mathrm{d}\theta) = \frac{Q}{2}\sin\theta\,\mathrm{d}\theta$$

All the components of the force exerted by this charge on the test charge cancel out, except for the one along the left-right axis, which is $F\cos\phi$. So, if you assume the electrostatic force law is $F = \frac{k q_1 q_2}{r^{2+\epsilon}}$, the force exerted by the charge in the shaded band on the test charge $q$ is

$$\mathrm{d}F = \frac{k q\,\mathrm{d}Q}{s^{2+\epsilon}}\cos\phi = \frac{kqQ}{2}\frac{\cos\phi\sin\theta\,\mathrm{d}\theta}{s^{2+\epsilon}}$$

Using the law of cosines you can calculate that

$$\begin{align}\cos\phi &= \frac{r^2 + s^2 - R^2}{2rs} & \cos\theta &= \frac{r^2 + R^2 - s^2}{2rR} \\ & & \sin\theta\,\mathrm{d}\theta &= \frac{s}{rR}\mathrm{d}s\end{align}$$

Substituting these into the expression for force and integrating gives you

$$F = \frac{kqQ}{4r^2R}\int_{R-r}^{R+r}\frac{s^2 + r^2 - R^2}{s^{2+\epsilon}}\mathrm{d}s$$

which works out to

$$F = \frac{kqQ}{2(1 - \epsilon^2)r^2R^{\epsilon}}\Biggl[\frac{(1+\epsilon \frac{r}{R})}{(1 + \frac{r}{R})^{\epsilon}} - \frac{(1-\epsilon \frac{r}{R})}{(1 - \frac{r}{R})^{\epsilon}}\Biggr]$$

A graph of this force as a function of $\frac{r}{R}$ and $0 < \epsilon < 1$ would look roughly like this:

In particular, it's negative, so the force is inward, and it gets larger as you approach the edge of the sphere. If $\epsilon > 0$, the force would be outward instead of inward, but other than being reflected over the x-axis the graph would be qualitatively similar.

If $\epsilon = -1$, then you have to do the integral a little differently because you're integrating $1/s$. You would then wind up with

$$F = \frac{kqQ}{2r^2 R}\biggl(rR - (R^2 - r^2)\operatorname{tanh}^{-1}\frac{r}{R}\biggr)$$

although the graph is still not qualitatively different; it's still positive and increases as you move away from the center of the sphere.