Faraday's Law from Lorentz force in the case of a moving conducting rod: how must the vectors be oriented?

Question

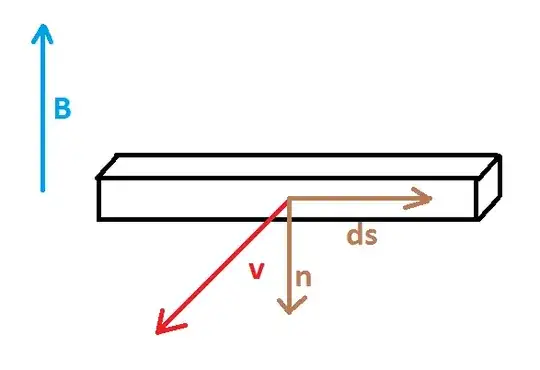
I'm confused on how to get Faraday Law from Lorentz Force in the following situation.

Consider a conducting rod moving with velocity $\bf{v}$ in a uniform (constant) magnetic field $\bf{B}$.

I think there are two vectors that must be chosen for the rod: the line vector $\bf{ds}$ and the normal vector $\hat{\bf{n}}$.

I oriented the two vectors in two different ways, but only in the first case I get to the law $$\mathrm{emf}=-\frac{\mathrm{d} \Phi(\bf{B})}{\mathrm{dt}}$$

correctly (i.e. with the minus sign).

I will show the reasoning in the two cases.

---

In both cases the Lorentz Force is $$\bf{F_L}=\mathrm{q} (\bf{v} \times \bf{B})$$

Which is equivalent to a field $$\bf{E_L}=\bf{v} \times \bf{B}$$

In order to get the $\mathrm{emf}$ I calculate the following integral

$$\mathrm{emf}=\int_{\mathrm{rod}} \bf{v} \times \bf{B} \cdot \bf{ds}=\int_{\mathrm{rod}} \bf{ds} \times \bf{v} \cdot \bf{B}=\int_{\mathrm{rod}} \bf{ds} \times \frac{\mathrm{d}\bf{l}}{\mathrm{dt}} \cdot \bf{B}= \bf{B} \cdot \frac{\mathrm{d}}{\mathrm{dt}}\int_{\mathrm{rod}} \bf{ds} \times \bf{dl}\tag{*}$$ Where $\bf{dl}$ is the infinitesimal displacement in the direction of $\bf{v}$.

Define a vector $\bf{dS}$ that represent the infinitesimal oriented area as $$\bf{dS}=||\bf{ds} \times \bf{dl}||\,\,\, \hat{\bf{n}}$$

And let $\bf{S}$ be the total oriented area, that is $$\bf{S}=\int ||\bf{ds} \times \bf{dl}||\,\,\, \hat{\bf{n}}$$

The two cases (with different orientation for $\hat{\bf{n}}$ and $\bf{ds}$) are different if I continue to work on expression $(*)$.

Case 1

Let the vectors be oriented as in picture

In this case $$\bf{ds} \times \bf{dl}=-\bf{dS}$$

Therefore $$\mathrm{emf}= \bf{B} \cdot \frac{\mathrm{d}}{\mathrm{dt}}\int_{\mathrm{rod}} \bf{ds} \times \bf{dl}=-\bf{B} \cdot \frac{\mathrm{d}}{\mathrm{dt}} \bf{S}=-\frac{\mathrm{d}}{\mathrm{dt}}(\bf{B} \cdot \bf{S})=-\frac{\mathrm{d\Phi} (\bf{B})}{\mathrm{dt}} $$

Case 2

Let the vectors be oriented as in picture

In this case $$\bf{ds} \times \bf{dl}=+\bf{dS}$$

Therefore $$\mathrm{emf}= \bf{B} \cdot \frac{\mathrm{d}}{\mathrm{dt}}\int_{\mathrm{rod}} \bf{ds} \times \bf{dl}=+\bf{B} \cdot \frac{\mathrm{d}}{\mathrm{dt}} \bf{S}=+\frac{\mathrm{d}}{\mathrm{dt}}(\bf{B} \cdot \bf{S})=+\frac{\mathrm{d\Phi} (\bf{B})}{\mathrm{dt}} $$

---

In Case 2 I do not get the proper minus sign: how can that be? Is there something wrong in what I have tried? In particular, is there any rule for which it is not correct to set the vectors oriented as in Case 2?

Answer 1

Before I answer your question, I want to point out a couple of "technical" mistakes in your proof.

1. The magnetic force on any charge is: F=q(v x B). Here, v is the NET velocity of the charge. In your proof you used the velocity of the rod, which is incorrect as the charges are moving with respect to the rod as well. Let that velocity be u. So the net velocity of the charges is v + u. But lucky for you the mistake doesn't matter, since u and ds are in the same direction, contributing nothing to the cross product.

2. Magnetic flux is calculated through a surface bound by a closed loop. In your case the closed loop is the wires and the imaginary surface is the area enclosed by the circuit. The emf in Faraday's law refers to the net electromotive force generated in the closed loop, which is in this case the ENTIRE circuit. What I'm trying to say is that your integral should be calculated along the entire closed loop, and not just through the part where the rod is located(put a circle on your integral sign). But again, since the rest of the circuit is not moving, what you did is not incorrect. The entire flux change is only due to the moving rod.

To answer your question in the simplest way possible, it all comes down to sign convention.

My second point above is of special importance for you to understand the answer. Look at the picture below. I have shown the two possible directions of the vector ds , the corresponding sense of integration over the entire circuit and the direction of the area vector in each case. Note that the direction of the area vector should be taken according to the "right hand curly thumb rule" (a name I made up). Curl the fingers of your right hand in your preferred direction of integration. Your thumb will point in the direction of the area vector of each elemental area(all have the same direction since your setup is planar).

In both cases you can see that the correct direction will be given by v x ds. Carry on, and you'll get your minus sign.

Answer 2

Define a surface $\:S\:$ (physical or imaginary) and its boundary closed curve $\:C\:$ . Define the unit normal vectors to the surface $\:\mathbf{n}\:$. These vectors define a direction $\:\overrightarrow{n_c}\:$ on the curve $\:C\:$ according to the right-hand rule. Define the magnetic flux through the surface $\:S\:$ \begin{equation} \Phi\equiv \iint\limits_{S}\mathbf{B}\boldsymbol{\cdot}\mathrm{d}\mathbf{S}=\iint\limits_{S}\left(\mathbf{B}\boldsymbol{\cdot}\mathbf{n}\right)\mathrm{d}\mathrm{S} \tag{01} \end{equation} Now, the emf in curve $\:C\:$ would induce a current $\:i_c\:$ which, according to Lenz Law, would have direction
\begin{equation} \text{direction of }\mathrm{i}_c= -\left(\text{sign of } \dfrac{\mathrm{d}\Phi}{\mathrm{d}t} \right)\times \left(\text{direction on curve } \overrightarrow{n_c} \right) \tag{02} \end{equation} so that the magnetic flux of the magnetic field produced by the current $\:\mathrm{i}_c\:$ would oppose the change in the magnetic flux due to EXTERNAL sources, as Kalyan comments under his answer:

Moreover, Lenz's law cannot be directly deduced from the minus sign alone. Lenz's law states that the induced emf will be in such a direction that it "opposes" the change in the magnetic flux due to EXTERNAL sources.

Note that the direction of the current $\:\mathrm{i}_c\:$ given by (02) is independent of the choice of the unit normal vectors $\:\mathbf{n}\:$. For if we choose the opposites \begin{equation} \mathbf{n'}=-\mathbf{n} \tag{03} \end{equation} then we have the opposite direction on the curve \begin{equation} \overrightarrow{n'_c}=-\overrightarrow{n_c} \tag{04} \end{equation} the opposite magnetic flux \begin{equation} \Phi'=\iint\limits_{S}\mathbf{B}\boldsymbol{\cdot}\mathrm{d}\mathbf{S}=\iint\limits_{S}\left(\mathbf{B}\boldsymbol{\cdot}\mathbf{n'}\right)\mathrm{d}\mathrm{S}=\boldsymbol{-}\iint\limits_{S}\left(\mathbf{B}\boldsymbol{\cdot}\mathbf{n}\right)\mathrm{d}\mathrm{S}=\boldsymbol{-}\Phi \tag{05} \end{equation} but the same direction of the induced current \begin{align} \text{direction of }\mathrm{i}'_c & = \boldsymbol{-}\left(\text{sign of } \dfrac{\mathrm{d}\Phi'}{\mathrm{d}t} \right)\times \left(\text{direction on curve } \overrightarrow{n'_c}\right)\\ & = \boldsymbol{-}\left(\boldsymbol{-}\text{ sign of } \dfrac{\mathrm{d}\Phi}{\mathrm{d}t} \right)\times \left(\boldsymbol{-}\text{ direction on curve } \overrightarrow{n_c}\right)\\ & = \text{direction of }\mathrm{i}_c \tag{06} \end{align}

Now, undoubtedly the magnitude of the emf in your question is \begin{equation} \vert \mathrm{emf}\vert=\begin{vmatrix} \boldsymbol{-}\dfrac{\mathrm{d}\Phi}{\mathrm{d}t}\end{vmatrix}=Bv\ell \tag{07} \end{equation} but its polarity is shown in the Figure below. The magnetic flux vector $\:\mathbf{B}\:$ is assumed constant pointing to the positive $\:z$-axis.

So, imagine that your rod is cylindrical rolling on two opposite sides of a rectagular wire. You have two surfaces of changing area, one back $\:S_b\:$, one front $\:S_f\:$. Applying Faraday Law with Lenz Law to any surface $\:S_\jmath \,(\jmath=b,f)\:$ with any unit normal $\:\pm\,\mathbf{n_\jmath}\,(\jmath=b,f)\:$ you will end up with the same result for the polarity of the motional emf.

Examples :

(1) If we define the unit normal to the back surface $\:S_b\:$ as $\:\mathbf{n_b}\:$ pointing to the positive $\:z$-axis, see Figure, then this vector defines an anti-clockwise (seen from the positive $\:z\:$) direction $\:\overrightarrow{\rm{EFCDE}}\:$ on the curve (rectangular) $\:\rm{EFCDE}$. The flux $\:\Phi_b\:$ through $\:S_b\:$ is increasing, $\:\mathrm{d}\Phi_b/\mathrm{d}t >0$, so that the direction of the hypothetical current $\:\mathrm{i}_b\:$, from which we'll conclude the emf polarity, is clockwise as shown in the Figure, since \begin{align} \text{direction of }\mathrm{i}_b & = \boldsymbol{-}\left(\text{sign of } \dfrac{\mathrm{d}\Phi_b}{\mathrm{d}t} \right)\times \left(\text{anti-clockwise } \right)\\ & = \boldsymbol{-}\left(\boldsymbol{+}\right)\times \left(\text{anti-clockwise } \right)\\ & = \text{clockwise} \tag{08} \end{align} Note that the lines of the magnetic flux density of the field produced by this hypothetical current $\:\mathrm{i}_b\:$ will cross the surface $\:S_b\:$ (that is the rectangle $\:\rm{EFCDE}$) with direction to the negative $\:z$-axis, opposing the increasing flux $\:\Phi_b\:$.

(2) If we define the unit normal to the front surface $\:S_f\:$ as $\:\mathbf{n_f}\:$ pointing to the negative $\:z$-axis, see Figure, then this vector defines a clockwise (seen from the positive $\:z\:$) direction $\:\overrightarrow{\rm{AEFBA}}\:$ on the curve (rectangular) $\:\rm{ABFEA}$. The flux $\:\Phi_f\:$ through $\:S_f\:$ is decreasing in magnitude but increasing in algebraic value, $\:\mathrm{d}\Phi_f/\mathrm{d}t >0$, so that the direction of the hypothetical current $\:\mathrm{i}_f\:$, from which we'll conclude the emf polarity, is anti-clockwise as shown in the Figure, since \begin{align} \text{direction of }\mathrm{i}_f & = \boldsymbol{-}\left(\text{sign of } \dfrac{\mathrm{d}\Phi_f}{\mathrm{d}t} \right)\times \left(\text{clockwise } \right)\\ & = \boldsymbol{-}\left(\boldsymbol{+}\right)\times \left(\text{clockwise } \right)\\ & = \text{anti-clockwise} \tag{09} \end{align} Note that the lines of the magnetic flux density of the field produced by this hypothetical current $\:\mathrm{i}_f\:$ will cross the surface $\:S_f\:$ (that is the rectangle $\:\rm{ABFEA}$) with direction to the positive $\:z$-axis, opposing the increasing flux $\:\Phi_f\:$.

Answer 3

Remember that flux is defined as $\vec{B} \cdot \vec{A}$.so if $\vec{B}$ and $ \vec{A}$ are in opposite directions it will simply result in a negative sign.thus your second case would reduce to the first case.

Your both approaches are correct.Let me explain how.

Let us consider a rod moving with velocity v .let the magnetic field point upwards.Look at the force that acts on an electron under the influence of the magnetic field. We may assume that velocity of the electron inside the conductor is same as that of the conductor itself.It is easy to see that the force on the electron is in +y direction.Hence an induced emf will act on the rod.Let us calculate this emf.

As you pointed out $$ emf=\int v\times B.dl$$Here it becomes necessary to define the direction of dl As we have already seen earlier the force on an electron inside the conductor is in +y direction.So it is evident that induced emf will be generated with its higher potential at the lower end.So we should choose the direction of dl as the -y direction.Now its turn to define the area vector.I will not repeat what you have already shown. $$B \frac{d}{dt}\int dl \times dl'$$ where dl' is the small displacement in the direction of velocity of rod.The direction of dl $\times$ dl' is +z.It is imperative that if we take the direction of normal vector as the -z direction it will reduce to your first case otherwise it will reduce to your second case.