2

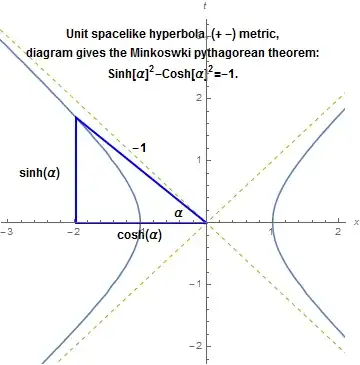
The SR invariance formula makes space-like intervals imaginary (e.g., the distance $x$ in a given frame has interval $ix$). Yet modern physicists consider it bad form to define the distance itself as $ix$, as Minkowski did. It seems to me that this distinction is trivial—what’s wrong with defining the distance as the value of its interval? An answer to a previous question of mine on this topic referred to a paper by Visser showing that there is a way to do this that can be generalized to GR. So what’s the fuss about? Even if there weren’t such a way, I don’t see how that would invalidate Minkowski’s definition for SR. Since the interval measure is what’s important, what fundamental difference can it make whether one defines the distance as x or as the imaginary interval $ix$?

The whole idea of a LT being an imaginary rotation (important, because phi is additive) depends on the use of the invariant measure, which is the complex length between two points in C2, the space in which complex rotations exist, and so the space in which the x-t plane is being considered to be embedded when we talk of complex rotations. In C2 it can easily be shown that the angle between any two axes, real or imaginary, is a real right angle, and this explains the invariance formula—it is simply the Pythagorean theorem for that complex triangle. So all this ‘invariant interval geometry’ is an integral part of special relativity. If you insist that distances are real and use a Pseudo-Euclidean metric, which would imply entirely different values for these angles, you are throwing out an enormous portion of SR. It is hard to see how that can be billed as an advance in our understanding.

Qmechanic
  • 201,751
murray denofsky
  • 268
  • 1
    Related post by OP: https://physics.stackexchange.com/q/305049/2451 Possible duplicates: https://physics.stackexchange.com/q/107443/2451 , https://physics.stackexchange.com/q/121380/2451 and links therein. – Qmechanic Apr 18 '17 at 04:28
  • Personally, to understand SR, I thought it was not until one knew how to physically create the SR phenomena, did one truly understand it. Physically creating SR, means that math is not required. But most folks choose not to go beyond the limits of math. And so arguments continue. https://www.youtube.com/watch?v=KKAwpEetJ-Q&list=PL3zkZRUI2IyBFAowlUivFbeBh-Mq7HdoQ – Sean Apr 22 '17 at 19:24

2 Answers2

8

Misner, Thorne, & Wheeler (MTW) offer arguments in"Farewell to ict" on Gravitation, p.51.

[updated with summary of their argument]

Reasons for using ict:

  1. It makes spacetime geometry look like Euclidean geometry.
  2. It make a Lorentz transformation look like a rotation.
  3. It allows one to avoid distinguishing components of a vector from its metric-dual one-form.

Reasons NOT to use ict:

  1. A vector is a very different geometric object from a one-form.
  2. The Euclidean angle is periodic, whereas the Minkowski-angle, better known as the rapidity ("velocity parameter"), increases monotonically without bound.
  3. Hiding the Lorentzian signature (- + + +) hides the light-cones that encode the causal structure.
  4. No one has discovered a way to use this in general relativity for a general curved spacetime manifold.
    and thus conclude:
    "If '$x^4 = ict$' cannot be used there, it will not be used here" [in this book Gravitation].

[end of update]

See page 19 of this 20-page excerpt at http://laplace.physics.ubc.ca/000-People-matt/200/gravitation.pdf.

robphy
  • 11,748
1

It is not uncommon for two descriptions in physics to be equivalent while one is preferred. If what you say about extending the $ict$ notion to general relativity is true, then there is no physical reason to prefer one or the other. Both are equivalent. On purely physical grounds, if two theories are isomorphic they're indistinguishable, and so are scientifically invalid. Here are a few counterarguments as for why the four-vector formulation is great:

  1. It links clearly to modern conventions for the discussion of differential geometry. One has a differentiable manifold with a topology (which gives a notion of two closeby points), a geometry (the metric and connection, which give notions of geodesics and parallel transport), and the vacuum einstein field equation $G_{\mu \nu}=0$.
  2. The algebraic structure of $\{i x : x\in \mathbb{R}\}$ is fragile. It's not a field or a ring or anything like that. You have to be careful or else you'll get complex coordinates everywhere! While you can make this work in special relativity and you assert it can be made to work in general relativity, at the very least it is a confusing pedagogical tool. It would be much more common to have students write "the light beam takes $1+i$ seconds to reach the detector" using complex times.
  3. The symmetry group of a $(+,-,-,-)$ metric is totally different than the symmetry group of a $(+,+,+)$ metric. You don't really get anything by pretending $SO(3,1)$ is an algebraic manipulation of $SO(4)$.
  4. You say "imaginary triangle", I say "Minkowski geometry". Potato potato. I think you're incorrect that "If you insist that distances are real and use a Pseudo-Euclidean metric, [that] would imply entirely different values for these angles." For example, the following diagram is one in Minkowski space for which $\alpha$ is a hyperbolic angle. The unit spacelike hyperbola takes the place of the unit circle. The "-1" is because the hyperbola is spacelike. The "$\alpha$" is the hyperbolic "angle".

Hyperbolic triangle

Personally, I think point number two is the most important one.

  • @user12029 Could you please clarify what exactly you mean by saying that "You don't really get anything by pretending SO(3,1) is an algebraic manipulation of SO(4)"? Their topologies are surely different, and so are their representations. So what? Is it impossible to establish a link? Where exactly will it break? Many thanks!! – Michael_1812 Jan 21 '23 at 05:18