We have the Euler equations for a rotating body as follows
$$I_1\dot\omega_1+\omega_2\omega_3(I_3-I_2)=0\\ I_2\dot\omega_2+\omega_1\omega_3(I_1-I_3)=0\\ I_3\dot\omega_3+\omega_2\omega_1(I_2-I_1)=0$$ Where $I_i$ are the moments of inertia about the $x_i$ axis, and $\omega_i$ is the angular velocity about this axis.
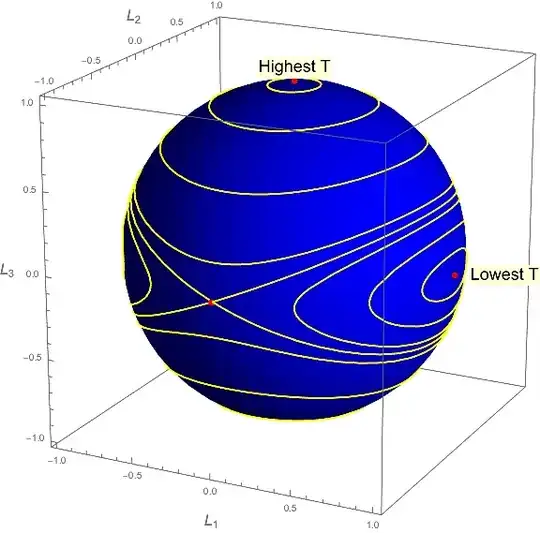
It can be shown (*) that if $I_1>I_2>I_3$, then objects with angular velocity very close to $\vec\omega=(0,1,0)$ are unstable. Why is this and how can I try to picture it?
I tried to picture this using a ball, but realised this is probably not a good way to visualise it, since a ball is spherically symmetric, so the moments of inertia are not distinct. Is there any visualisation or animation that could allow me to see this rotation, and possibly understand why it is unstable?
(*) In response to @SRS's comment:
I am not sure about any references, but I know how to do it: Let $\omega_1=\eta_1,\omega_3=\eta_3$ where $\eta$ is a small perturbation, and suppose $\omega_2=1+\eta_2$. Then the Euler eqns become$$I_1\dot\eta_1=(I_2-I_3)\eta_3+O(\eta^2)\tag1$$$$I_2\dot\eta_2=O(\eta^2)\tag2$$$$I_3\dot\eta_3=(I_1-I_2)\eta_1+O(\eta^2)\tag3$$Differentiate $(1)$ and sub in $(3)$ to the resulting expression$$\ddot\eta_1=\frac{(I_2-I_3)(I_1-I_2)}{I_3I_1}\eta_1$$If $I_1>I_2>I_3$, then the constant on the right hand side is positive, so the solution to this equation is an exponential (if it was any other order, then the solution would be a $\sin/\cos$). Therefore it is unstable.
Edit:
To clarify, I posted this question to see other more visual ways of understanding this effect rather than solving the equations as I did above, and to see how this effect comes into play in real life. So I don't think it is a duplicate of the other questions, since they don't have answers that fit this.

https://www.youtube.com/watch?v=PY7fRozbrtk
https://www.youtube.com/watch?v=-Si6iRL5Fj8
3, https://www.youtube.com/watch?v=4dqCQqI-Gis (with an actual tennis racket). See https://en.wikipedia.org/wiki/Tennis_racket_theorem for the analytical work.
– ZeroTheHero Apr 05 '18 at 21:12