The question is as follows:
Consider a point charge Q placed at $(0,h,0)$ (Cartesian coordinates). Find the flux in an area formed by $y=0$, $z\leq0$, $x\geq l$ and $x\leq a$ $( l\leq x\leq a )$.
I tried this by considering the two extreme lines $x=l$ and $x=a$ and I constructed a cylinder (infinitely long) using the plane passing through $y=h$ and $x=l$. Then I tried taking some angles but I was unable to find any symmetry in the situation.
Can someone please help me solve this?
If Q is a point charge in empty space then the flux through a surface $\:S\:$ is \begin{equation} \Phi=\dfrac{\Theta}{4\pi}\dfrac{Q}{\epsilon_{0}} \tag{01} \end{equation} where $\:\Theta\:$ is the solid angle(*) by which the point Q "sees" the surface $\:S$.
Now, if $\:0=\ell \leq a \:$ and the strip has a finite height $\:b\:$ along the negative $\:z\:$ then according to the Proposition-Practical Rule in my answer here we have (Figure 01) \begin{equation} \tan\Theta\left(b\right)=\dfrac{s}{h\!\cdot\!d}=\dfrac{a\!\cdot\!b}{h\!\cdot\!\sqrt{a^{2}+b^{2}+h^{2}}} \tag{02} \end{equation} so for an infinite strip (Figure 02) \begin{equation} \tan\Theta=\lim_{b\rightarrow \infty}\tan\Theta\left(b\right)=\lim_{b\rightarrow \infty}\dfrac{a\!\cdot\!b}{h\!\cdot\!\sqrt{a^{2}+b^{2}+h^{2}}} \nonumber \end{equation} that is \begin{equation} \boxed{\:\:\color{blue}{\tan\Theta=\dfrac{a}{h}}\:\:} \qquad 0=\ell \leq a \tag{03} \end{equation}
If $\:0<\ell \leq a \:$ then we must subtract from the solid angle $\:\Theta_{1}\:$ of the infinite strip of width $\:a \:$ the solid angle $\:\Theta_{2}\:$ of the infinite strip of width $\:\ell \:$ \begin{equation} \Theta=\Theta_{1}-\Theta_{2} \tag{04} \end{equation} But \begin{equation} \tan\Theta_{1}=\dfrac{a}{h} \quad \text{and} \quad \tan\Theta_{2}=\dfrac{\ell}{h} \tag{05} \end{equation} so \begin{equation} \tan\Theta=\tan\left(\Theta_{1}-\Theta_{2}\right)=\dfrac{\tan\Theta_{1}-\tan\Theta_{2}}{1+\tan\Theta_{1}\tan\Theta_{2}}=\dfrac{\dfrac{a}{h}-\dfrac{\ell}{h}}{1+\dfrac{a}{h}\dfrac{\ell}{h}} \tag{06} \end{equation} that is (Figure 03) \begin{equation} \boxed{\:\:\color{blue}{\tan\Theta=\dfrac{h\left(a-\ell\right)}{h^{2}+a\ell}}\:\:} \qquad 0<\ell \leq a \tag{07} \end{equation}
If $\:\ell<0 \leq a \:$ then we must add to the solid angle $\:\Theta_{1}\:$ of the infinite strip of width $\:a \:$ the solid angle $\:\Theta_{2}\:$ of the infinite strip of width $\:\vert\ell\vert=-\ell \:$ \begin{equation} \Theta=\Theta_{1}+\Theta_{2} \tag{08} \end{equation} But \begin{equation} \tan\Theta_{1}=\dfrac{a}{h} \quad \text{and} \quad \tan\Theta_{2}=\dfrac{\vert\ell\vert}{h}=\dfrac{-\ell}{h} \tag{09} \end{equation} so \begin{equation} \tan\Theta=\tan\left(\Theta_{1}+\Theta_{2}\right)=\dfrac{\tan\Theta_{1}+\tan\Theta_{2}}{1-\tan\Theta_{1}\tan\Theta_{2}}=\dfrac{\dfrac{a}{h}-\dfrac{\ell}{h}}{1-\dfrac{a}{h}\dfrac{-\ell}{h}} \tag{10} \end{equation} that is \begin{equation} \boxed{\:\:\color{blue}{\tan\Theta=\dfrac{h\left(a-\ell\right)}{h^{2}+a\ell}}\:\:}\qquad \ell<0 \leq a \tag{11} \end{equation} Combining (03),(07) and (11) we have in general \begin{equation} \boxed{\:\:\color{brown}{\tan\Theta=\dfrac{h\left(a-\ell\right)}{h^{2}+a\ell}}\:\:}\qquad \ell\leq a,\quad a\ge 0 \tag{12} \end{equation}
(*) Examples of solid angles $\:(\rho\pi, \rho=1/4,1/2,1,2,4)\:$ are shown in the the Figure Solid Angles under my answer here : Flux through side of a cube.
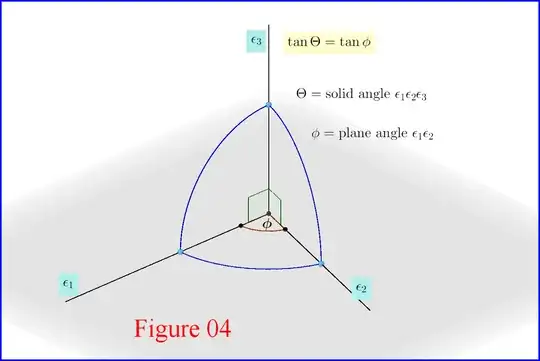
An other method to find a solution to this specific problem is based on the fact (could be proved easily) that in case of a solid angle $\:\Theta\:$ formed by three rays $\:\epsilon_{1},\epsilon_{2},\epsilon_{3}\:$ with $\:\epsilon_{3}\:$ normal to the plane of $\:\epsilon_{1},\epsilon_{2}\:$ (Figure 04) we have \begin{equation} \Theta=\phi \quad \Longrightarrow \quad \tan\Theta=\tan\phi \tag{13} \end{equation} where $\:\phi\:$ the plane angle formed by the rays $\:\epsilon_{1},\epsilon_{2}$. These are the cases of Figures 02 and 03.
