We have to find flux due to a point charge at $(0,l,0)$ on an infinite strip lying in region $(0,0,0)$, $(l,0,l)$ and extending to infinity along $+x$ direction.
I am aware that a general case has been explained here, but that uses integration beyond high school mathematics. Can this be done by taking a gaussian surface or something?
My attempt: Take an infinite cuboid with the surface as its base and height $l$, with $q$ charge at one of its vertices. So $$\frac{q}{8}$$ would be enclosed. As three sides of the cuboid are in contact with charge and the side at infinity would not experience any flux, the remaining two sides would experience flux. And that too in equal magnitude as they lie symmetrically. Thus $$\frac{q}{8 \epsilon} = \phi$$
Thus flux through one surface comes out to be $$\frac{q}{16\epsilon}$$ But the answer is given as $$\frac{q}{48\epsilon}$$ How can we do this question?
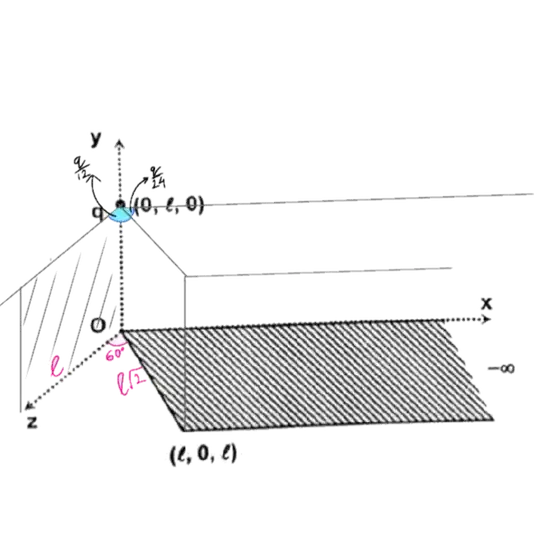It has q/24 charge enclosed in the cuboid, so flux is q/48.