Describe supersymmetry to a non-physicist in few sentences

Question

Can someone help me describe the idea of supersymmetry in a few sentences, to a broad scientific audience? That is, a science or engineering graduate student who hasn't studied much theoretical physics may understand.

Answer 1

In particle physics, supersymmetry (SUSY) is a principle that proposes a relationship between two basic classes of elementary particles: bosons, like the Higgs boson or the force carriers (photons, gluons, hypothetically graviton), which have an integer-valued spin, and fermions like the electron or the quarks, which have a half-integer spin.

Under supersymmetry, a fermion must exist for every boson and a boson for every fermion.

Answer 2

In classical physics, objects, even tiny particles of matter, can be characterized by their mass and charge. The mass is a variable depending on the density of the material and the charge is measurable , whether neutral or not, following classical electrodynamics. One can define energy and momentum and angular momentum vectors, depending on the particular problem and its boundary conditions which follow classical mechanics.

The elementary particles, out of which all macroscopic matter is composed, follow quantum mechanics, where the equations do not solve for trajectories but define probability distributions, not orbits, orbitals. Studying elementary particle interactions has defined the particles in a very specific way. They have a fixed mass and charge, and an intrinsic angular momentum called spin, which characterizes them.

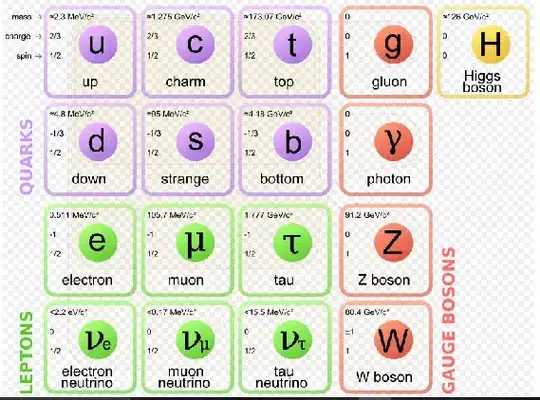
Here is the presently known table:

They have either integer spin (bosons) or half integer spin (fermions).

This is the standard model, and this standard model has the accompanying antiparticle table ( which is usually not displayed) which has the same mass as the particles table but opposite quantum numbers, so when particle antiparticle meets there is only energy left , and new pairs can be freely created. All this has been experimentally validated over and over again.

Supersymmetry is the proposal that for each particle in the table there exists a supersymmetric partner which has a specific spin, bosons become fermions and fermions become bosons in this scheme.

The reason this theory has been proposed is to regulate the mathematical behavior of the models that predict the interactions of elementary particles at high energies, which have infinities that can be cancelled by the use of a supersymmetric model. Supersymmetry is important in string theory models , which aim to unify all four interactions, but that is another story.

Answer 3

The supersymmetry is a symmetry of the superspace which is our usual spacetime extended by several Grassmanian coordinates. Unlike the usual numbers the product of two Grassmanian numbers anticommute i.e. change the sign if you change the order i.e. $\theta_1\theta_2=-\theta_2\theta_1$.

This is the most important thing about the supersymmetry. The supersymmetry is an extension of the spacetime symmetry, not just some tricky symmetry between various types of particles. Moreso it is the only extension of the usual spacetime symmetry in the quantum models considered sensible.

Because this is the extension of the spacetime symmetry the supersymmetry transformation can change the fields tranforming in one way under usual spacetime symmetries into the fields transforming in a different way. For example take the vector that should be rotated when you go into the rotated coordinates. After a specific supersymmetry transformation it may become the scalar that doesn't change at all! What's interesting is that the supersymmetry also transforms such fields that in self-consistent quantum models are usual numbers (strictly speaking commuting operators) into the less-familiar fields with spinor indices that should be described by the Grassmanian numbers.

On the particle language those transformation properties correspond to the property named the spin that corresponds to a polarization of the field excitation. The scalars, vectors and other tensor fields describe the particles with integer spins and wavefunctions symmetric under exchange of the particles - bosons. In the macroscopic physics the bosons tend to condensate together and start behaving as ordinary classical fields so usually we recognize them as "carriers of interactions". The spinor fields describe the particles with half-integer spins and wavefunctions antisymmetric under exchange of the particles - fermions. In the macroscopic physics the fermions tend to behave more as classical particles and we usually recognize them as "matter". The supersymmetry transformation changes the spin of the particles and can change bosons into fermions.

To conclude with several key phrases:

• The supersymmetry is a symmetry of the superspace which is a spacetime with several anticommuting Grassmanian coordinates
• Because it is the extended spacetime symmetry it can change the tranformation properties of the objects under usual spacetime symmetries
• That's why it relates to each other bosons (responsible for "interactions") and fermions ("matter"), wildly different from the ordinary point of view
• This is the only way to extend the usual spacetime in sensible quantum models