Electric field on rim of uniformly charged disk

Question

What is the electric field on (or near) the rim of a uniformly charged disk? I know how to find the electric field along the central axis at a certain point away on that axis from the uniformly charged disk (negligible thickness), but there was an example in my E&M textbook (Purcell and Morin) where they calculated the electric potential on the rim of said disk due to other charges on the disk and it ended up being $$\phi = \frac{\sigma a}{\pi \epsilon_{0}}. $$ By using the Gradient theorem saying that electric field is the negative gradient of electric potential, is it true that it is just zero as you take the partial of the above electric potential with respect to $r$? How can this be if the electric field points outwards/"up" from the center of the disk towards the rim pushing charges upwards towards the edges of the disk -- isn't this nonzero, or do all the vectors cancel out to 0 in which case how are those charges pushed to the rim in the first place if the net electric field at that point is 0?

Answer 1

The field at the rim is infinite.

The simplest way to calculate the potential and the field at the rim is to introduce Cartesian coordinates in which the center of the disk is not at the origin but at $(a,0)$. Then we will calculate quantities at the origin, which is a typical point on the rim.

To actually do the integrals, use polar coordinates $(r,\theta)$. To integrate over the disk, the $\theta$ coordinate will range from $-\pi/2$ to $\pi/2$, and the $r$ coordinate can be shown to range from $0$ to $2a\cos\theta$. (To see this, draw a diagram and do the trig.)

The potential at the origin (on the rim) is

$$\varphi=k_e\int\frac{\sigma\,dA}{r}$$

where $k_e$ is the electric constant ($1/4\pi\epsilon_0$ in SI units; $1$ in Gaussian units). The area element is $dA=r\,dr\,d\theta.$ So we get the known potential

$$\varphi=k_e\sigma\int_{-\pi/2}^{\pi/2}d\theta\int_0^{2a\cos\theta}dr=4k_e\sigma a.$$

The field integral at the origin (on the rim) is

$$E_x=-k_e\int\frac{\sigma\,dA \cos\theta}{r^2}$$

which is divergent:

$$E_x=-k_e\sigma\int_{-\pi/2}^{\pi/2}\cos\theta\,d\theta\int_0^{2a\cos\theta}\frac{dr}{r}=+\infty.$$

ADDENDUM:

For a more complicated but more complete approach...

In cylindrical coordinates $(\rho,\phi,z)$ centered on the disk, the potential at any point can be shown to be

$$\varphi(\rho,z)=2\pi k_e\sigma a\int_0^\infty\frac{dk}{k}e^{-k|z|}J_0(k\rho)J_1(ka)$$

where the $J_m(x)$ are Bessel functions of the first kind.

Special cases are easy to compute:

The potential at the center of the disk is

$$\varphi(0,0)=2\pi k_e\sigma a\int_0^\infty\frac{dk}{k}J_1(ka)=2\pi k_e\sigma a\,\big(1\big).$$

The potential at the rim is lower by a factor of $2/\pi$:

$$\varphi(a,0)=2\pi k_e\sigma a\int_0^\infty\frac{dk}{k}J_0(ka)J_1(ka)=2\pi k_e\sigma a\,\left(\frac{2}{\pi}\right).$$

The potential along the $z$-axis (a standard homework calculation by a simpler approach) is

$$\varphi(0,z)=2\pi k_e\sigma a\int_0^\infty\frac{dk}{k}e^{-k|z|}J_1(ka)=2\pi k_e\sigma a\,\left(\frac{\sqrt{a^2+z^2}-|z|}{a}\right).$$

In the disk’s plane where $z=0$, the integral gives a function of $\rho$,

$$\varphi(\rho,0)=2\pi k_e\sigma a\left\{ \begin{array}{ll} \frac{2}{\pi}E\left(\frac{\rho^2}{a^2}\right), & \rho<a \\ \frac{2}{\pi}\left[\frac{\rho}{a}E(\frac{a^2}{\rho^2})+\frac{a^2-\rho^2}{a\rho}K(\frac{a^2}{\rho^2})\right], & \rho>a, \end{array} \right.$$

where $K(k)$ and $E(k)$ are complete elliptic integrals of the first and second kind.

This can be shown to have infinite slope at $\rho=a$. However, this is not particularly obvious when graphing the potential, which looks like this, where the horizontal axis is $\rho/a$ and the vertical axis is in units of $2\pi k_e\sigma a$:

One can also see that the field is infinite by computing the gradient of the potential inside the integral. That procedure produces for $\rho=a$ and $z=0$ an integral involving Bessel functions which is divergent.

ADDENDUM 2:

For even more completeness...

One finds that the field in the $z=0$ plane is given by

$$E_\rho=2\pi k_e\sigma a\left\{ \begin{array}{ll} \frac{2}{\pi\rho}\left[K(\frac{\rho^2}{a^2})-E(\frac{\rho^2}{a^2})\right], & \rho<a \\ \frac{2}{\pi a}\left[K(\frac{a^2}{\rho^2})-E(\frac{a^2}{\rho^2})\right], & \rho>a \end{array} \right.$$

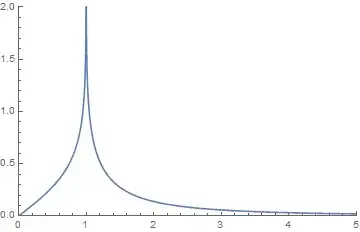
The function to the right of the brace looks like this, where the horizontal axis is $\rho/a$:

The divergence at the rim is because $K(1)$ is infinite.