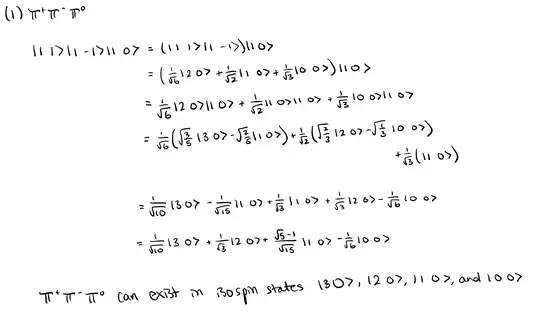I've been calculating the possible isospin states for $\pi^0\pi^+\pi^-$ state and get this as my final answer after referencing the Clebsch Gordan Coefficients table:
$$\frac{1}{\sqrt{10}}|30\rangle+\frac{1}{\sqrt{3}}|20\rangle+\frac{\sqrt{5}-1}{\sqrt{15}}|10\rangle-\frac{1}{\sqrt{6}}|00\rangle$$
However, if I square the magnitudes in front of the kets and sum them, I don't get one, and this is because of the factor of $\frac{\sqrt{5}-1}{\sqrt{15}}$ which comes from the fact that I added the $\pi^+\pi^-$ first, which gave a $|20\rangle$, $|10\rangle$, and $|00\rangle$ state. Adding the $\pi^0$ to this gives a state of $|10\rangle$ from both adding $|2 0\rangle|10\rangle$ and $|00\rangle|10\rangle$, which gives me that factor of $\frac{\sqrt{5}-1}{\sqrt{15}}$ in total. Is there any reason why the sum of the squares doesn't add to one? Or is my calculation wrong? Here's all of my work if it helps: