4

We can measure only rational numbers by our scale. Here is an example where irrational numbers does makes sense. If so then this question may have some theoretical importance. Is irrational numbers important for physics?

Community
  • 1
Self-Made Man
  • 1,945
  • Do you mean "sensitive to irrational numbers" but "not sensitive to rational ones"? $\pi$ and $\sqrt 2$ and $e$ show up all the time in physics. Are you imagining (for example) a process where if $\alpha$ were exactly $1/137$ things would be completely different than if it's an irrational number really close to $1/137$? – Brandon Enright May 10 '13 at 18:49
  • Do you mean imaginary numbers? – DilithiumMatrix May 10 '13 at 18:51
  • 1
    An example would be pseudo-random optical lattices! If you have a superposition of two standing waves with wave-lengths $\lambda_1$ and $\lambda_2$, then if they are truly incommensurable, the resulting standing wave is non-periodic and can be considered "random" or "disordered", whereas if they are commensurable, i.e., if their ratio is a rational number, the lattice is still periodic (albeit with a possibly large period) – Lagerbaer May 10 '13 at 18:53
  • @BrandonEnright: although $\pi$ occurs very often, I've hardly ever seen $e$ as a pure number. Most often we use it by convention, for example instead of measuring the entropy as $S = k \ln \Omega$ we could just as well write $S = k' \log_{13} \Omega$ for some rescaled Boltzmann constant $k'.$ – Vibert May 10 '13 at 18:57
  • These two types have different mathematical character. Is that difference proved important in any physical theory? @BrandonEnright – Self-Made Man May 10 '13 at 18:58
  • Related: http://physics.stackexchange.com/q/20822/2451 , http://physics.stackexchange.com/q/38184/2451 – Qmechanic May 10 '13 at 19:02
  • Antoher example, closely related to what @Lagerbaer suggests are quasi-crystals. Again, the key word is "commensurability" – Slaviks May 10 '13 at 19:18
  • 'Irrational speed' - sounds like when my brother drives! – Qmechanic Nov 07 '15 at 13:06

2 Answers2

4

One of the directions to look at goes under the name of "commensurability". Imagine electrons that can travel on a two-dimensional lattice and suppose there is a constant magnetic field perpendicular to the lattice. Making a discrete loop on the lattice will add to the electron-wavefunction an Aharonov-Bohm phase propotrional to the area coverd by the loop. Resulting interference pattern will depend on the commensurability of the enclosed magnetic flux with the flux quantum $h/e$.

The spectrum of electrons on a lattice under as a function of magnetic field has a beautiful fractal shape known as Azbel'-Hofstadter butterfly:

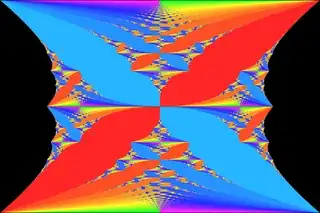
enter image description here

The way I see it relates to OP's question is that this spectrum has no bands if the magnetic field takes irrational values in appropriate units. Of course, since any measurement/realization precision is finite, rationals with large irreducible denominators would be indistinguishable form true (mathematical) irrationals. But I think it it still as close as it gets to physical relevance of (ir-)rationality.

Slaviks
  • 4,413
0

How about the [Feigenbaum constants?],1 I'm not sure if they have been proven irrational though. Anyone know btw?

Mauchy
  • 101