You have already got some good answers.
But I would like to add some more concrete and visual explanations
for convincing you. This can be done with Newtonian mechanics and
elementary geometry only, but without the advanced mathematics
usually used in general relativity.
Here is a table with some trajectories of balls
thrown up with velocity $v$, reaching maximum height $h$,
and total time of flight $T$.
Using Newtonian mechanics (with $g=10\text{ m/s}^2$) we have
$$h=\frac{v^2}{2g} \tag{1}$$ and
$$T=\frac{2v}{g} \tag{2}.$$
\begin{array}{c|c|c|c|c}
v & h & T & cT & R \\ \hline
1\text{ m/s} & 0.05\text{ m} & 0.2\text{ s} & 6\cdot 10^7\text{ m} & 9\cdot 10^{15}\text{ m} \\ \hline
10\text{ m/s} & 5\text{ m} & 2\text{ s} & 6\cdot 10^8\text{ m} & 9\cdot 10^{15}\text{ m} \\ \hline
100\text{ m/s} & 500\text{ m} & 20\text{ s} & 6\cdot 10^9\text{ m} & 9\cdot 10^{15}\text{ m} \\ \hline
\end{array}
We need to analyze the trajectory not in 3-dimensional space,
but in 4-dimensional space-time (with $ct$ as the 4th coordinate,
$c=3\cdot 10^8\text{ m/s}$ being the speed of light). Therefore the table above also
contains the values of $cT$.
Our goal is to find the curvature radius $R$ in 4-dimensional space-time.
We can draw the curved trajectory in space-time ($z$ versus $ct$).
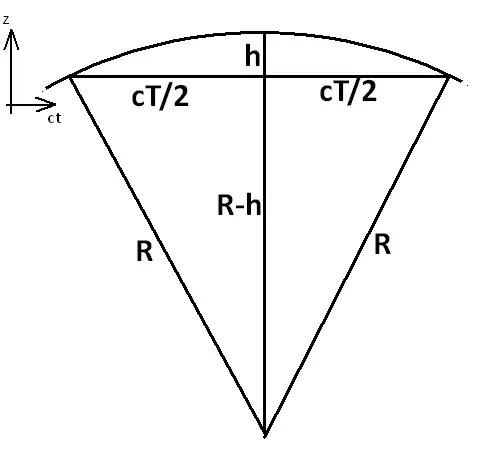
Of course this drawing is not to scale.
Because of the huge value of $cT$
the curved trajectory at the top would be much less curved,
and the center of curvature would be much further down.
But it is enough for analyzing the geometry.
Applying Pythagoras' theorem to the right triangle we get:
$$\left(\frac{cT}{2}\right)^2+(R-h)^2=R^2$$
or
$$\left(\frac{cT}{2}\right)^2+R^2-2Rh+h^2=R^2$$
The $R^2$ cancels out. We can neglect the small $h^2$
and resolve for $R$:
$$R=\frac{(cT)^2}{8h} \tag{3}$$
The calculated values of this curvature radius $R$ are also
shown in the table above. It turns out, the radius $R$ is huge (nearly one light year)
and (may be as a surprise) completely independent of the trajectory.
To understand how this comes about, we can insert
$h$ and $T$ from (1) and (2) into (3).
We find
$$R=\frac{c^2}{g} \tag{4}$$
This relation makes evident:
The curvature of the trajectory in 4-dimensional
space-time depends only on gravity $g$ and nothing else.
Especially it is independent of the initial velocity $v$.
