How can a force vector be shifted laterally when it is a sliding or a bound vector?

Question

Question:

One end of a rope of length $l$ is attached to a vertical wall, the other end being attached to a point on the surface of a uniform sphere of radius $a$. If the weight of the sphere is $W$, then show that the tension of the rope is $T=\frac{W(l+a)}{\sqrt{2al+l^2}}$.

My tutor's attempt:

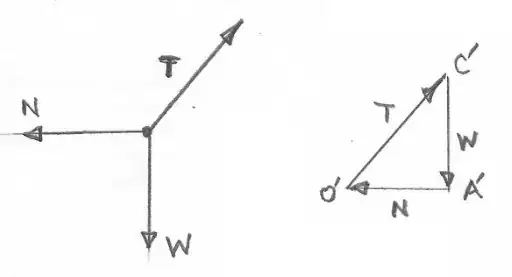
$$\text{We shift $\vec{W}$ to the line segment CA}\tag{1}$$

Now,

$$OC=OB+BC$$

$$OC=a+l$$

And,

$$OA=a$$

Now,

$$OC^2=OA^2+AC^2$$

$$AC^2=(a+l)^2-a^2$$

$$AC^2=a^2+2al+l^2-a^2$$

$$AC^2=2al+l^2$$

$$AC=\sqrt{2al+l^2}$$

Now, comparing $\vec{N}$, $\vec{T}$ and the shifted $\vec{W}$ with $\triangle AOC$,

$$\frac{N}{a}=\frac{T}{l+a}=\frac{W}{\sqrt{2al+l^2}}$$

$$[\text{If three forces acting at a point are in equilibrium then the sides of any triangle taken in order parallel to the forces will be proportional to the forces}]$$

Using 2nd and 3rd fractions,

$$\frac{T}{l+a}=\frac{W}{\sqrt{2al+l^2}}$$

$$T=\frac{W(l+a)}{\sqrt{2al+l^2}}\ \text{(showed)}$$

My book's attempt:

Using Lami's theorem,

$$\frac{T}{\sin(90^{\circ})}=\frac{W}{\sin(180^{\circ}-\angle COA)}$$

$$T=\frac{W}{\sin(\angle COA)}$$

$$T=\frac{W}{\frac{CA}{CO}}$$

$$T=\frac{W}{\frac{\sqrt{2al+l^2}}{a+l}}$$

$$T=\frac{W(l+a)}{\sqrt{2al+l^2}}\ \text{(showed)}$$

My comments:

I think my tutor's attempt is wrong (no offense intended to him) and my book's is right, even though both were able to prove the question statement. My tutor in $(1)$ shifted $\vec{W}$ to $CA$. How can he do that? Isn't force only a sliding vector or a bound/localized/fixed vector? As my tutor shifted $\vec{W}$, I think my tutor is wrong.

On the contrary, my book did the math easily and accurately in my opinion.

My question:

Isn't my tutor's attempt wrong as he shifted $\vec{W}$?

The same post exists on Math SE. I thought resident physicists of Physics SE might be more suited to answer the question, so I posted it here too. — tryingtobeastoic, Mar 08 '22 at 05:05
Please note that homework-like questions and check-my-work questions are generally considered off-topic here. We intend our questions to be potentially useful to a broader set of users than just the one asking, and prefer conceptual questions over those just asking for a specific computation. — Níckolas Alves, Mar 08 '22 at 05:16

Farcher · Accepted Answer · 2022-03-08T09:09:02.710

Nothing wrong as to what your teacher did except perhaps not explain enough what was being done to your satisfaction.

On the left is the free body diagram for the sphere showing the three forces acting on the sphere.

On the right is the vector addition triangle to show the resultant of the three forces is zero.

The only thing to add is that situation triangle $OAC$ is similar to force triangle $O'A'C'$ because all three angles are the same.
This means that the ration between the sides is the same for both triangles.

Your teacher omitted drawing the force triangle.

See also my answer to this post, Static Equilibrium Problem with 3 Tension Forces

How can a force vector be shifted laterally when it is a sliding or a bound vector?

1 Answers1